Understanding fractions can be tricky, but converting them into mixed numbers makes it easier to visualize their value. Take 9/8 for instance—this improper fraction might seem daunting at first glance, but it’s a straightforward concept once broken down.
In this article, readers will discover how to transform 9/8 into a mixed number and why this conversion is useful in everyday math. Mixed numbers not only simplify calculations but also enhance comprehension of fractional values. By the end, anyone will feel more confident tackling similar fractions.
Table of Contents
ToggleUnderstanding Mixed Numbers
Mixed numbers consist of a whole number and a proper fraction combined. They provide a clear way to represent values greater than one while incorporating fractional components.
Components of Mixed Numbers
- Whole Number: Represents complete units. For example, in the mixed number 1 1/8, the whole number is 1.
- Proper Fraction: Denotes the remaining part of the whole. In 1 1/8, the proper fraction is 1/8.
Conversion Process
Convert an improper fraction into a mixed number by following these steps:
- Divide the numerator by the denominator. For instance, 9 divided by 8 equals 1.
- Identify the remainder. In this case, the remainder is 1.
- Combine the quotient and remainder to form the mixed number. Thus, 9/8 becomes 1 1/8.
Applications
Understanding mixed numbers aids in various mathematical scenarios. They enhance comprehension in cooking, measurements, and everyday tasks that involve fractions. Mixed numbers make calculations more intuitive, especially in contexts where whole units are needed alongside fractional parts.
Converting 9/8 to a Mixed Number

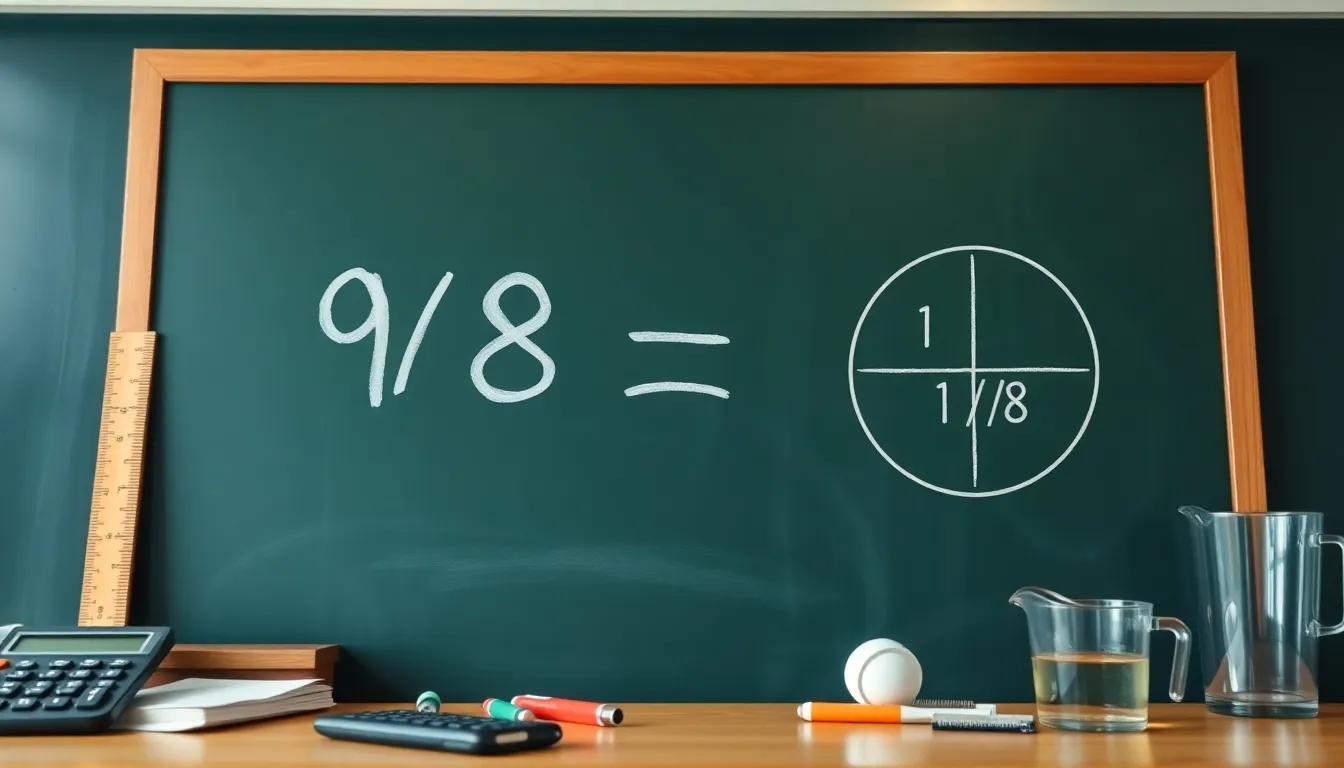
Converting the improper fraction 9/8 into a mixed number involves a straightforward process. This conversion aids in better understanding and working with fractional values.
Step-by-Step Process
- Divide the numerator by the denominator.
Divide 9 by 8, resulting in a quotient of 1.
- Identify the remainder.
Subtract the product of the quotient and the denominator from the numerator:
( 9 – (8 times 1) = 1 ).
The remainder is 1.
- Form the mixed number.
Combine the quotient and the remainder over the original denominator:
( 1 frac{1}{8} ).
Thus, 9/8 converts to the mixed number 1 1/8.
Importance of Proper Conversion
Proper conversion of improper fractions into mixed numbers enhances clarity in mathematics. Mixed numbers provide a more intuitive representation of quantities greater than one, facilitating easier computations in practical scenarios. Additionally, grasping mixed numbers enriches understanding in fields such as cooking, crafting, and construction, where precise measurements are crucial. By converting fractions correctly, individuals can communicate values more effectively in everyday situations.
Properties of 9/8 as a Mixed Number
9/8 as a mixed number provides valuable insights into the properties of improper fractions. Understanding these properties enhances comprehension and application in various mathematical contexts.
Comparison with Other Fractions
9/8 compares interestingly with various fractions. It represents a value greater than whole numbers like 1 and less than 2. In contrast to 1/2 and 3/4, which signify lesser values, 9/8 shows the difference in size. It provides a better sense of measurement than improper fractions alone. By converting 9/8 to 1 1/8, the whole part (1) indicates there’s one complete unit, while the proper fraction (1/8) signifies a portion beyond that unit. This distinction simplifies mathematical operations and fosters clearer comparisons with fractions and whole numbers.
Visual Representation
Visualizing 9/8 as a mixed number helps clarify its value. A number line illustrates this effectively. Marking 0, 1, and 2 on the line, the position of 9/8 occurs slightly beyond 1 but before 2, showing its proximity to the whole number. A pie chart can also convey the fraction’s meaning, with one whole pie representing the whole part and a separate section illustrating 1/8 of an additional pie. These visual aids facilitate understanding, making it easier to grasp the concept of mixed numbers in practical applications.
Practical Applications
Mixed numbers like 9/8 find relevant use in various real-world scenarios, enhancing comprehensibility and practical skills.
Real-World Examples
- Cooking Recipes: Recipes often require fractional measurements. For instance, a recipe calling for 9/8 cups of flour translates to 1 1/8 cups, streamlining the process for home cooks.
- Construction Projects: When measuring materials, such as lumber, mixed numbers simplify the representation of lengths. A measurement of 9/8 inches clarifies that the length is slightly more than one inch, aiding in accurate cuts.
- Crafting: Crafters frequently deal with mixed numbers while working with fabrics and decorative materials. Understanding 9/8 yards of fabric means they know they need just over one yard.
- Gardening: Gardeners use mixed numbers to express quantities of soil or mulch needed, making calculations simpler for acreage planning. For 9/8 cubic yards of soil, it’s easier to visualize as 1 1/8 cubic yards.
Relevance in Math Education
- Conceptual Understanding: Mixed numbers help students grasp the relationship between fractions and whole numbers, making it easier to visualize and manipulate numbers.
- Problem-Solving Skills: Learning to convert improper fractions fosters essential problem-solving skills. Students often encounter these in practical math applications, reinforcing their understanding of the subject.
- Improved Communication: Expressing values like 9/8 in a mixed form aids students in communicating mathematical ideas clearly and accurately, enhancing classroom discussions.
- Curriculum Standards: Many educational standards emphasize the importance of understanding mixed numbers, allowing students to meet curriculum goals in fractions and measurement.
Through these practical applications, the mixed number 1 1/8 provides a clear, functional representation of quantities in daily tasks and educational environments.




